The FFP Machine Implemented With An FPGA
Edit: If you're interested in reduction machines for functional programs in general, especially ones that work and have had three years of development as opposed to three weeks, checkout these guys: The Reduceron.Edit 2: Also check out this Non-Von Neumann computer!
As I previously hinted, I worked on an FFP Machine recently for a school project. Unfortunately I only had about three weeks to work on it (along with everything else going on), so that time was largely spent just understanding the FFP Machine, and I didn't get very far in the code. (The code referenced in the paper to download doesn't even compile to Verilog yet, and I've actually scrapped what's there in a new project that I'll share if I work more on it. Also, the school won't have copyright over the new project.)
So my paper is largely a summarization of what the FFP Machine is and does, along with a collection of the best resources I found out there in case you want to learn more. I also may convert parts of it into a Wikipedia page since once does not currently exist for the FFP Machine. If you have any questions (or want any of the papers in the sources) feel free to email me (see the About page at the top), though I can't guarantee I'll be able to help. Anyway, below is my Paper in HTML form, for the benefit of Google and for my own word-count tracker. If you want to read on, I highly recommend reading the PDF version outputted from LaTeX. It is uploaded here.
The FFP Machine Implemented With An FPGA - Kevin Secretan
Abstract
While researching hardware specializations for functional programming such as the LISP Machine, I discovered several papers on the Formal Functional Programming (FFP) Machine. The architecture relies on a set of small-grain processors working concurrently on a program expression to reduce it to an answer, which made the project a good candidate for implementation on an FPGA. I proceeded to implement the necessary parts of the FFP Machine, however as of this writing I have not finished a programmable version. With a few more man-days of work, it would still be a limited implementation meant as proof-of-concept and groundwork for future projects. I found it difficult to build as this was my first large-scale project using an FPGA, though I can describe the intended functionality of program reduction in action and explain the parallelism. This paper will focus on a summary of what the FFP Machine is and some implementation details.
1 Introduction
1.1 Goal
The goal of this project was to implement the necessary pieces of the FFP Machine and demonstrate the functionality to an enough extent that it serves as a proof of concept. The project involved learning about hardware design languages in general, learning the architecture of the FFP Machine, and building it. Due to time constraints a fully general form of the machine could not be built, but I aimed to lay the groundwork to potentially build upon in the future. The source code is in Python using the MyHDL library so it can be extended and edited easily for future work.
I first heard of the FFP Machine while researching hardware implementations for Scheme, a dialect of Lisp. I found the dissertation Three Implementation Models for Scheme[3], which as its third implementation discusses compiling Scheme to the FFP Language for execution on the FFP Machine. To my knowledge, the FFP Machine has never before been implemented on an FPGA, and any implementations at all do not exist in a form that I can access. The dissertation DOT: A distributed operating system model of a tree-structured multiprocessor[2] provides many useful implementation details for building and simulating the FFP Machine and reasoning about the performance of programs written for it, but nevertheless the paper does not reveal an actual implementation to "try at home".
1.2 Background
1.2.1 The FFP Language and Machine
The FFP Machine is an architecture designed to execute programs written in the FFP language, first specified by John Backus in his Turing Award Lecture Can Programming Be Liberated from the von Neumann Style? A functional Style and its Algebra of Programs.[1] The FFP language is a (formal) functional programming language similar to Lisp but with many syntactic sugaring removed in order to make it suitable for machine execution. The language works via program reduction rather than evaluation, and by implementing it in a parallel environment such as an FPGA board it can do many operations normally considered to take linear time (such as summing a list of numbers) in constant time.
A simple FFP program is (+ :<4, 6, 8>) which reduces to the value 18. From this simple program an intuition can be formed of what syntactical elements the FFP Language has available to it: all expressions start with a left parenthesis and are immediately followed by a function (or a sub-expression that reduces to a function), such as +, which will correspond to a "machine code" primitive executed by the FPGA, which for the case of this project is written in MyHDL. The colon separates the function from its arguments, and the angle brackets denote a list whose elements are separated by commas. At present the user of my implementation must write the FFP program in a slightly lower-level fashion, but a compiler to that lower-level shouldn't require too much work. Rather than spend time on that, however, it might be better to design a string interpreter directly on the FPGA to evaluate strings on the fly and avoid any compilation at all!
1.2.2 Further Reading
Gyula Magó produced an excellent paper[6] called The FFP Machine which goes into the nitty-gritty details of the architecture and overall design of the FFP Machine and has served as my primary reference, and also is where the examples given in this paper come from. This paper presents a heavily summarized view of the FFP machine and deals more with the specific HDL implementations of the parts I got working rather than the system as a whole.
2 Methods, Techniques, and Design
2.1 Software
2.1.1 Tools
Originally the goal was to use straight Verilog to implement the FFP Machine, since it was known and compilation was simple using Quartus' IDE. As I learned more about Verilog, however, I discovered MyHDL which provides a mechanism for writing Python code that compiles down to either Verilog or VHDL. I chose to use MyHDL instead as the syntax is cleaner, I have access to Python's power, and certain historical warts involving blocking vs. non-blocking statements and dealing with signed vs. unsigned integers in Verilog could be avoided. In the end I compile everything down to Verilog for final loading into Quartus' IDE which can program Altera's DE2 FPGA development board with my FFP Machine and some program to run.
2.1.2 Building
In order to build a program in the FFP Language and load it onto my FFP Machine, it is necessary to write the principal representation of the FFP expression yourself and stick it into the top_level.py module, then run Python with the MyHDL module to convert it into Verilog which you can then use to program an FPGA. Future work on this step includes having a routine in Verilog that can read the program off an SD card instead of bundling it with the FFP Machine itself.
2.2 FFP Machine Design
This is a summary of the FFP Machine architecture described by Magó in his The FFP Machine paper. At the highest level, an FFP Machine consists of an interprocess communication network of T-cells (Tree) connected at the Leaves to an array of L-cells.
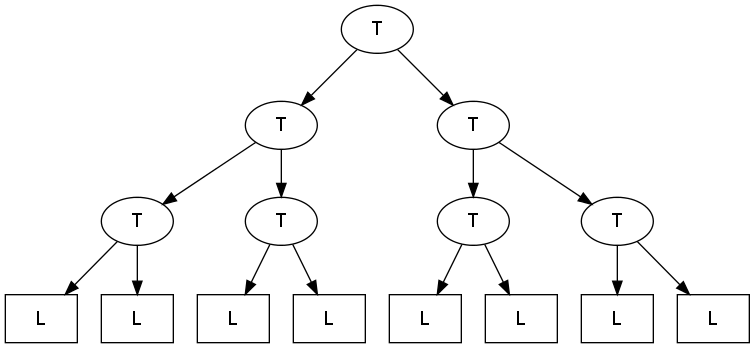
Figure 1: FFP high-level overview.
Each L-cell holds exactly one symbol in the FFP expression, hence the program
(+ :<4, 6, 8>) is represented in the array of L-cells, called the Principal Representation, as:
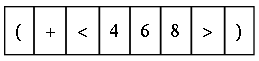
Figure 2: Principal Representation of a program
Note that since each L-cell holds one symbol this reduces the FFP language syntax, no longer requiring colons (since the first symbol after a parenthesis is either a function or a sub-expression that reduces to a function) or commas (since the boundaries of the L-cell act as delimiters).
The Auxiliary Representation of a program is constructed dynamically within the L-cells, and it consists of three pieces of data: some number of selectors, a relative level number (rln), and an index. To illustrate this form of expression, I will use the more interesting program (TR : <<2, 4, 6>, <3, 5, 7>>) where TR is the matrix transpose function.
Figure 3 helps explain selectors, which designate the path to reach some node if the principal representation is made into a tree. Hence the path (2,1,2) represents the number 4, while the path (1) denotes the function TR. (The path could also be represented as (1,0,0), since 0's denote an end.) The RLN is seen as the height of the node in the tree, and the index is simply the index into the array of L-cells for each item. Table 1 shows both the principal representation of this program and the auxiliary representation information.
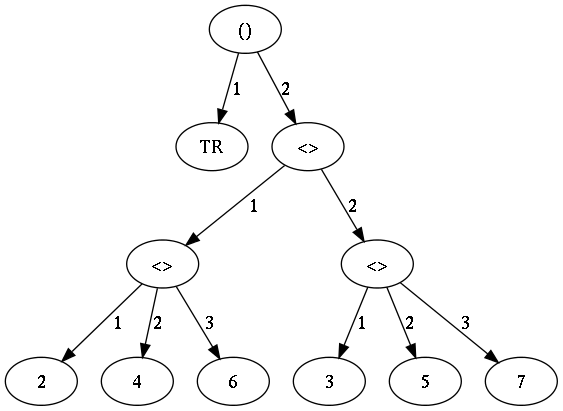
Figure 3: The tree-form of the FFP expression (TR : <<2, 4, 6>, <3, 5, 7>>). Edges of the tree are the selector values.
Principal: ( TR < < 2 4 6 > < 3 5 7 > > )
1st selector 0 1 2 2 2 2 2 2 2 2 2 2 2 2 0
2nd selector 0 0 0 1 1 1 1 1 2 2 2 2 2 0 0
3rd selector 0 0 0 0 1 2 3 0 0 1 2 3 0 0 0
rln 0 1 1 2 3 3 3 2 2 3 3 3 2 1 0
index 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Table 1: Auxiliary Representation of (TR : <<2, 4, 6>, <3, 5, 7>>)
Computing the auxiliary representation is described further on.
2.3 Running a program
One machine cycle consists of three phases: partitioning, execution, and storage management. This corresponds to having a global phase Signal in HDL that can activate different branches of code.
Partitioning is where the machine locates any programs that can be reduced, then partitions the communication network of T cells to match up with the L cells to reduce. The actual actions it does in the T-network are described later on.
Execution consists of initialization, which will only happen once, and actual execution which may be suspended and resumed in a further machine cycle. Initialization consists of requesting whatever primitive program is needed if an L-cell contains a function, creating the auxiliary representation of the program, and receiving the L-cell primitive. The execution part executes the local program it received by communicating in the T-cell network with message waves, and at the end either requests extra space and suspends execution. My implementation does not contain the space-request feature. The primitive code that is run is different than a standard program and may also use the T-cell network for processing, though not always.
Storage management changes the principal representation in the L-array by erasing cells and rewriting values, also creating empty L-cells and moving things around if any were requested by the execution phase. My implementation just does the remapping then scans for any singular result it can bring back to display on the output.
2.4 Message passing
2.4.1 T Cells
The partitioning phase sets the two partitioning switches (shown in Figure 4) in each T cell to one of four possible configurations (shown in Figure 5). The configurations determine which messages can be sent by the two children of each T cell, and they are determined by whether or not subtrees contain parentheses which denote reducible programs.
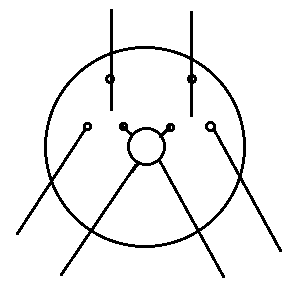
Figure 4: Shows the partitioning switches. The inner circle is a message processor.
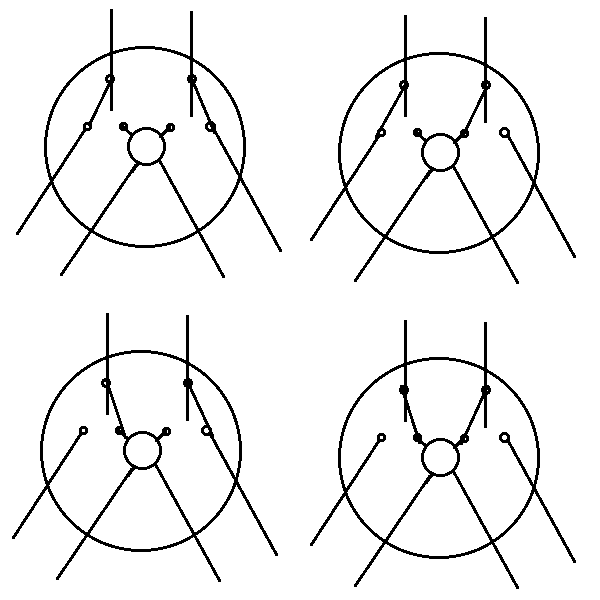
Figure 5: The four partitioning configurations whose leaf nodes contain some portion of an application.
Partitioning is done in a parallel operation where each L-cell sends its information about parentheses up the network of trees. Each T-cell in turn processes the information in the two child-messages and sends it up to its parent T-cell. By the time it reaches the root node, the partitioning has been completed.
Switches are set according to whether subtrees contain parentheses: if the left (and correspondingly right) subtree contains no parentheses, the left (and respectively right) partitioning switch of the T cell is set to the inward position.
Each message consists of one of five possible values (encoded as 0 through 4 (requiring 3 bits)) depending on the information about its children nodes:
- -- : there are no parentheses in the subtree
- (): the leftmost parenthesis is "(" and the rightmost is ")"
- ((: the leftmost is "(" and the rightmost is "("
- )): the leftmost is ")" and the rightmost is ")"
- )(: the leftmost is ")" and the rightmost is "("
For the programs I'm interested in initially demonstrating the messages will be either -- or () at the top of the tree. A handy guide to determine which message packet should be sent to the parent is given in Table 2. (If a subtree contains only one parenthesis, then it's both left and rightmost, so this happens at the T cells closer to the L-cells.)
R X L -- () (( )) )(
-- -- () (( )) )(
() () () (( () ((
(( (( () (( ()* ((*
)) )) )) )( )) )(
)( )( )) )( ))* )(*
Table 2: Computing which message to send to the parent T-cell, the horizontal axis is the right subtree, the vertical axis is the left subtree. The four items marked with an asterisk designate that the sending T-cell is an effective "root".
2.5 Computing Auxiliary Representation
The auxiliary representation is computed using the T-cells. Each L-cell sends an upsweep message through the network and when that message hits a root node, that root broadcasts a message in a downsweep back to each L-cell which stores the necessary data. Thus it only takes logarithmic time in the number of L-cells to compute the values.
On the upsweep, if a comes in the left child of a T cell and b comes in on the right child communication channel, the T cell sends a+b up to its parent. On the downsweep, if the number d comes in from the parent, the T cell sends d to its left child and a+d (hence it must store a on the upsweep) to its right child. The root node starts with d = 0.
The index computation for this implementation is trivial because it is already known at compile-time, and so it will just be "baked in" to the L cell on creation. (The user must feed in the principal representation as an array at compile-time.) As the program is reduced, however, calculating the index is as simple as making a cumulative sum through each element in the L array.
The relative level number is trickier to calculate. For each element a in the L array, take the input ai = 1 if the L cell holds an opening bracket or parenthesis, ai = -1 if the L cell holds a closing bracket or parenthesis, and ai = 0 otherwise. The cumulative sum gives the RLN at each node, except for those holding opening parentheses and angle brackets, which are one above what they should be, so subtract one from them to fix it. The highest RLN computed is the number of selectors there will be.
Computing the selectors is done first by defining RLN' = 0 if the L cells hold closing parentheses or angle brackets, RLN' = RLN otherwise. A tuple of booleans is then sent as input to the L cell; the tuple's length is the max height of the tree, and the tuple's values are (if the height is 3) <RLN' == 1, RLN' == 2, RLN' == 3>, which corresponds to (by summing up each element) <S1',S2',S3'>. The tricky part here is that S2' resets to 0 if RLN1' == 1, and S3' resets to 0 if RLN2' == 1. After all is done, each Si is the value of Si' if the RLN is larger than or equal to i, and 0 otherwise. (Thus for example a < at RLN level 2 will always have 0 as its third selector.)
2.6 HDL Representations
The source code implemented so far is fairly complicated, see below for where to retrieve it. For a brief summary, a T-cell contains 6 different Signals: a generic msg path, the signal line from its left child and from its right child, a signal line to its parent, a signal line controlling the direction of the sweep, and a signal line signaling the phase of the machine cycle. It has storage for its position switch status and whether or not it is a root node.
An L-cell contains signals for the parent T-cell to send messages and the machine phase. It contains storage for the symbol itself, the index, the RLN, and its selectors (the last three determined in the execution phase with the help of the T-cell parent).
2.6.1 Primitive programs
L-cells request programs to act on or with them. The primitive programs implemented in HDL (or in this case, a mixture of Python and HDL) can be thought of as programmed in the Leaf-cell Programming Language (LPL).
So far, only APNDL (append-to-the-left), LENGTH, and + are implemented. APNDL is defined as a simple boolean equation: if (S1 < 2) or (S2 = 2 and S3 = 0), then erase the FFP symbol. LENGTH is defined as each L-cell sending its last selector up the tree, and the max is the result which is stored in the application symbol (all other L-cells are erased). + is defined as each L-cell sending itself and summing takes place along the way up the T-cell network, with the root node finally containing the result and sending it back down to store in the application symbol and erasing all other L-cells. These examples illustrate why the auxiliary representation is so important: it helps the LPL language be parallel and fast.
3 Design Verification
The ultimate goal for demonstrating the FFP Machine in action is to reduce the program IP === <CMP,+,<ATA,*>,TR> which computes the Inner Product of two arrays. The symbol CMP designates the Composition rewrite rule. It works as: (<CMP,f1,f2, ... ,fn>:x) --> (f1:(f2:( ... (fn:x) ... ))). The symbol ATA defines the rewrite rule "Apply to all" which works as: (<ATA,f>:<x1,x2, ... ,xn>) --> <(f:x1),(f:x2$), ... ,(f:xn)> (this is analogous to Scheme's apply procedure). The symbol TR is the primitive function Transpose, which is the same as a mathematical matrix transpose.
The program I wish to verify therefore is: (IP:<<1,2,3>,<3,4,5>>). Following Magó in his article, the reduction is as follows. By the definition of IP, the program becomes (this should be done by the compiler but must currently be done by the user)
(CMP,+,<ATA,*>,TR>:<<1,2,3>,<3,4,5>>).
By the definition of CMP, this becomes
(+:(<ATA,*>:(TR:<<1,2,3>,<3,4,5>>))).
By the definition of TR, this becomes
(+:(<ATA,*>:<<1,3>,<2,4>,<3,5>>)).
By the definition of ATA, this becomes
(+:<(*:<1,3>),(*:<2,4>),(*:<3,5>)>).
By the definition of *, this becomes (+:<3,8,15>) which by the definition of + becomes 26.
If a result can be obtained from the FFP Machine, its lowest bits are to be displayed on the red LEDs of the Altera FPGA demo board, with an on-light symbolizing 1. Hence after running the above the result should show the sequence "11010".
Unfortunately this ultimate goal was too complicated to get working in the time available (rewrite rules are not implemented in the compiler or FPGA), so simpler programs are used instead, such as the final addition line, but even they do not yet run since the machine is not in a programmable state and needs further work.
As a testament to the elegance of the FFP Language, however, here for comparison is an equivalent inner product program expressed in the Python programming language: sum(k*v for (k,v) in zip(*[(1,2,3),(3,4,5)])). (zip(*matrix) acts as the transpose function.) Note that both Python and FFP support a language elegance not found in most low-level languages like C or various assemblies, and the FFP version enjoys a highly parallelized execution environment making it faster. (Magó actually defines a parallelized IP primitive in his paper.)
4 Discussion
4.1 Scope
This was really a semester-project at best rather than a month-long project (especially the final month of school), therefore the full objectives I had planned in the beginning were not realized and even my conservative estimates of what I would accomplish were not conservative enough. At best this is a starting point for a much larger project implementing the full machine with supporting tools, and may serve as a useful collection of resources for understanding the FFP machine and getting started on its implementation.
The choice of MyHDL was also motivated by its heavy unit testing library in order to prove the correctness of my design, which if I had used it from the beginning may have helped get a programmable version up and running.
4.2 Implications for a successful implementation
One of the turn-offs from GPU programming is the low-level nature in which it must usually be done. A fully implemented FFP Machine provides a more pleasing interface to work with while maintaining the high parallelism people use GPUs for. It may even be worthwhile to explore implementing an FFP Machine on an existing GPU which may support certain optimizations a typical FPGA does not easily do.
4.3 Source code
The source code, figures, and LaTeX file for this paper can all be found at
http://www.thejach.com/public/ffp_machine.zip
5 Conclusions and Future Work
While falling pretty far short of the original goals, I still consider the project to be useful as grounding for future improvements that I have mentioned off-hand previously. There is proof-of-concept here and the parallel execution can be demonstrated in argument through the use of the computed auxiliary representation.
An immediate improvement (after getting it in a programmable state anyway) would be to extend the set of primitive instructions to the full richness described in Magó's paper. An interesting improvement would be writing a Scheme to FFP compiler, which presents interesting challenges due to high level features of Scheme such as continuations, closures, and recursive calls of anonymous lambda functions. In spirit with creating a Scheme compiler, another possibility is to implement an APL compiler which this paper[4] details.
Another obvious improvement is designing a system for program loading from an SD card, which may actually be straight-forward using the NiOS core packaged with Quartus tools. One could further use SD as extended memory for holding all the L cells.
The machine in general can be optimized as well. Magó discusses different compression methods for representing the FFP expression, though he does not use them later in his paper. Other optimizations have been outlined by other individuals, such as this paper[7] describing "An architecture for fast data movement in the FFP machine". Magó has another paper describing a more efficient method of data sharing within the FFP machine[5].
6 Acknowledgments
- Thanks to Nick Rivera, for instructing me on Verilog and HDL-in-general.
- Thanks to Jeremy Thomas, for providing me with some of the papers I needed.
- Thanks to Gyula Magó, wherever you are these days, for writing clearly on the FFP Machine and making it an interesting thing to learn about.
References
- J. Backus. Can Programming Be Liberated from the von Neumann Style? A functional Style and its Algebra of Programs. Communications of the ACM, 21, 8, pages 613--641,
1978. URL:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.72.2622&rep=rep1&type=pdf. - S. Danforth. DOT, A Distributed Operating System Model of a Tree-Structured Multi-processor. PhD thesis, University of North Carolina at Chapel Hill, 1983. URL:
http://www.cs.unc.edu/Publications/full_dissertations/danforth_dissertation.pdf. - R. Kent Dybvig. Three Implementation Models for Scheme. PhD thesis, University of North Carolina at Chapel Hill, 1987. URL: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.66.786&rep=rep1&type=pdf.
- Alexis Koster. Compiling APL for parallel execution on an FFP machine. SIGAPL APL Quote Quad, 15:29--37, May 1985. URL: http://portal.acm.org/citation.cfm?doid=255315.255327.
- Gyula Magó. Data sharing in an FFP machine. In Proceedings of the 1982 ACM symposium on LISP and functional programming, LFP '82, pages 201--207, New York, NY, USA, 1982. ACM. URL: http://doi.acm.org/10.1145/800068.802151.
- Gyula Magó and Donald F. Stanat. The FFP Machine. In High Level Language Computer Architecture, pages 430--468. Computer Science Press, 1989. URL:
http://www.amazon.com/High-level-language-computer-architecture-Advances/dp/0881751324. - David Plaisted. An architecture for fast data movement in the FFP machine. In Jean-Pierre Jouannaud, editor, Functional Programming Languages and Computer Architecture, volume 201 of Lecture Notes in Computer Science, pages 147--163. Springer Berlin / Heidelberg, 1985. 10.1007/3-540-15975-4_35 URL: http://dx.doi.org/10.1007/3-540-15975-4_35.
Posted on 2011-05-04 by Jach
Tags: FFP Machine, FPGA, HDL, programming
Permalink: https://www.thejach.com/view/id/172
Trackback URL: https://www.thejach.com/view/2011/5/the_ffp_machine_implemented_with_an_fpga
Recent Posts
2026-01-06
2025-12-31
2025-11-10
2025-10-15
2025-08-18