Mesh Current Method
Suppose you are given this circuit topology: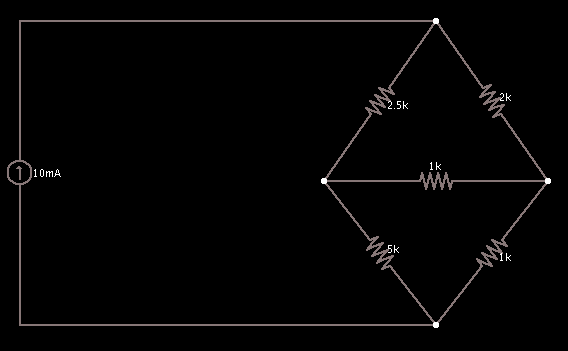
What is the power dissipated by the 1 k-ohm resistor in the center?
You can use any of several techniques for answering this problem, but the simplest is the Mesh Current Method; you'll only have two equations to solve. The Mesh Current Method is based off of Kirchoff's Voltage Law which states that the sum of voltage rises and drops in a closed loop is zero. This allows us to draw three different "meshes", as we have three loops:
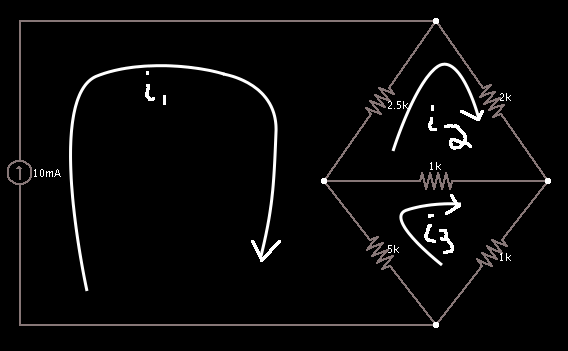
We drew three different currents around each loop, using a clockwise convention.
We can now write Kirchoff's Voltage Law around each loop, remembering that [math]V = I*R[/math] and substituting in our known values. This would give us three equations and three unknowns, but wait, the circuit contains a current source, so we already know the value of i1!
This leaves us with two equations and two unknowns, namely i2 and i3. When we know both of these currents, we can calculate the power of the resistor since [math]P = I*V = I^2*R[/math] and we'll know the total current through that resistor.
Let's write our two equations, using the convention that we have a voltage drop on a resistor whose sign is negative:
[math]
\begin{eqnarray}
0 &= -2.5(i_2 - i_1) - 2i_2 - 1(i_2 - i_3) \\
0 &= -5(i_3 - i_1) - 1(i_3 - i_2) - i_3
\end{eqnarray}
[/math]
Equation 1 is around the loop with i2. It is very important to notice the currents on the shared resistors. Obviously the 2 k-ohm resistor is only affected by the i2 current, but the 2.5 k-ohm resistor is also affected by the i1 and so we have to deal with that consequence. The currents i2 and i1 are traveling in opposite directions at the 2.5 k-ohm resistor, so the consequence is i1 is subtracted from i2. Similarly for the shared 1 k-ohm resistor in the middle which is affected by i3.
Note in Equation 2 the shared 1 k-ohm resistor has the current multiplier of i3 - i2, the opposite of equation 1. Why is that? Because the sign convention has changed. This time, i3 designates a positive going current, and i2 is in the opposite direction of the loop's convention, forcing the subtraction.
Remember we know the value of i1 = 10 mA, so after substituting and reducing we are left with:
[math]
\begin{eqnarray}
5.5i_2 - i_3 &= 25 \\
-i_2 + 7i_3 &= 50
\end{eqnarray}
[/math]
Note that these equations should be intuitive and can be arrived at by inspection. Here is the circuit again:

For the first equation, what resistors does the loop's current affect? All three, which is why we have 5.5 = 2.5 + 2 + 1 as its coefficient. How many resistors does i3 affect? Just the 1 k-ohm one, which is its coefficient. And our current source? It affects the 2.5 resistor, which is where our 25 = 10*2.5 comes from.
Similarly for the second equation, i2 shares the middle resistor, i3 touches all of its three (7 = 5+1+1), and i1 touches just the 5 k-ohm one (50 = 10*5).
The signs are also intuitive. For the first equation, only i2 is positive (move the 25 back over and see that the 10mA carried a negative sign with it). For the second equation, only i3 is positive.
Solving this system reveals that i2 = 6 mA and i3 = 8 mA.
Pause a moment and consider the units and how we ended up at mA. I was pretty sloppy in my equations by keeping the units hidden, and if you think about it, shouldn't the several 103's and 10-3's cancel each other out? I apologize for the sloppiness, but it's important to train yourself to think of the units without seeing the units as even textbooks commonly leave them out here and there. Consider it like removing the key names on a keyboard in order to learn touch typing.
The answer to the last question is no, they don't (all) cancel out. In the reduced form of equation 1, there are two hidden 103's attached to each current, due to the effects of a kilo-ohm resistor. The two unknown mesh currents are in amps from the equation's point of view. Imagine we just had this form:
[math]i (A) * 2*10^3 (ohms) = 10 (V=A*ohms)[/math]
Solving for i:
[math]i (A) = \frac{10 (A*ohms)}{2*10^3 (ohms)} = 5 * 10^{-3} (A) = 0.005 (A)[/math]
Now it's simply recognizing that (mA) = 103 * (A), which is what is going on in the two solved equations.
Okay, we have the currents, let's get back to what was originally asked. How much power is dissipated by the 1 k-ohm resistor in the middle?
[math]P = I^2*R = (6mA -8mA)^2 * 1k\Omega = 4 mW[/math]
So, 4 milliwatts of power. (Notice that here we have 10-3 squared, making the factor from the resistor only remove one milli.)
Fairly straightforward, right? Two equations, two unknowns, just be careful with units and everything will be alright. But now I want to know: how much power is produced by the current source? Here is the circuit yet again:

We could try and come up with an equivalent resistance to our crossed diamond in the diagram, using a delta-y conversion and other such ugliness, but we don't need to. We can simply exploit the fact that in a circuit, the total amount of power produced is equal to the total amount of power consumed. Resistors consume power, so we can simply figure out the amount of power consumed by each resistor (as we know the necessary currents involved for our I2R equation), and we have our answer. Using our calculated power and finding the power for the other resistors is trivial. Just be careful you have considered the total currents on each resistor!
[math]2.5 * (6-10)^2 + 2*6^2 + 4 + 5*(8-10)^2 + 1*8^2 = 200 mW[/math]
Therefore 200 milliwatts are produced and it's up to you to decide if you like to represent produced power with a negative sign or not.
The Mesh Current Method is a great tool to have in your box, it's really fast once you get the hang of it, calculators are excellent for solving systems of equations quickly (and Cramer's rule is alright for that too), and the method can even be done intuitively and by inspection as mentioned above.
Extra Credit: What if we changed the current source to a voltage source of 10 volts? Simply make the first i1 mesh around the outermost (through the 2k and 1k resistors) or innermost (through the 2.5k and 5k resistors) loop! You decide!
Posted on 2011-03-11 by Jach
Tags: circuit analysis, computer engineering
Permalink: https://www.thejach.com/view/id/158
Trackback URL: https://www.thejach.com/view/2011/3/mesh_current_method
Recent Posts
2025-11-10
2025-10-15
2025-08-18
2025-08-16
2025-07-31