Playing with Morton Numbers
Dimensionality is a lie... okay, it's more of an interpretation.If you have a set of integers such that you can construct coordinate pairs (x,y) (such as the locations of the pixels on your screen), this set of pairs is said to have two dimensions. But there's no reason it can't have three: the third dimension is just always 0! (x, y, 0). And so on for any upper dimension.
What about scaling it down to 1 dimension though? Is that even possible? Turns out, yes, and it's pretty easy. Just convert each x and y to base 2, and interleave the bits such that all of x's bits are in even positions and y's bits are in odd positions. We call the resulting binary number a Morton Number.
Does this really work though? What this suggests is that all (x,y) pairs have a 1-to-1 mapping with the simple set of integers in one dimension. (Say x.) If that is true, then that means the number of (x,y) pairs is equivalent to the number of possible x or y individually. In standard nomenclature, the cardinality of the two sets is the same, that of the set of integers.
How can we prove a 1-to-1 mapping? The standard way is to show that $$f(x) = f(y) \to x = y$$. We need to define our Morton Number function!
Let X be the minimal binary representation of x, and Y for y. Pad X or Y with 0s until their binary representation length is equal; The Morton Number M then has twice that length. Start the most significant bit of M with the most significant bit of Y, then alternate bits of Xs and Ys. With that established, let's try all cases for x = 0..3 and y = 0..3 to see if we can find a pattern.
$$(0,0) \Rightarrow X = 0, Y = 0 \Rightarrow M = 00 = 0$$
$$(0,1) \Rightarrow X = 0, Y = 1 \Rightarrow M = 10$$
$$(0,2) \Rightarrow X = 00, Y = 10 \Rightarrow M = 1000$$
$$(0,3) \Rightarrow X = 00, Y = 11 \Rightarrow M = 1010$$
$$(1,0) \Rightarrow X = 1, Y = 0 \Rightarrow M = 01 = 1$$
$$(1,1) \Rightarrow X = 1, Y = 1 \Rightarrow M = 11$$
$$(1,2) \Rightarrow X = 01, Y = 10 \Rightarrow M = 1001$$
$$(1,3) \Rightarrow X = 01, Y = 11 \Rightarrow M = 1011$$
$$(2,0) \Rightarrow X = 10, Y = 00 \Rightarrow M = 0100 = 100$$
$$(2,1) \Rightarrow X = 10, Y = 01 \Rightarrow M = 0110 = 110$$
$$(2,2) \Rightarrow X = 10, Y = 10 \Rightarrow M = 1100$$
$$(2,3) \Rightarrow X = 10, Y = 11 \Rightarrow M = 1110$$
$$(3,0) \Rightarrow X = 11, Y = 00 \Rightarrow M = 0101 = 101$$
$$(3,1) \Rightarrow X = 11, Y = 01 \Rightarrow M = 0111 = 111$$
$$(3,2) \Rightarrow X = 11, Y = 10 \Rightarrow M = 1101$$
$$(3,3) \Rightarrow X = 11, Y = 11 \Rightarrow M = 1111$$
Hmm... There seems to be a definite pattern! Let's sort by M:
0000 (0,0)
0001 (1,0)
0010 (0,1)
0011 (1,1)
0100 (2,0)
0101 (3,0)
0110 (2,1)
0111 (3,1)
1000 (0,2)
1001 (1,2)
1010 (0,3)
1011 (1,3)
1100 (2,2)
1101 (3,2)
1110 (2,3)
1111 (3,3)
This doesn't help me that much... maybe we should try and plot it?
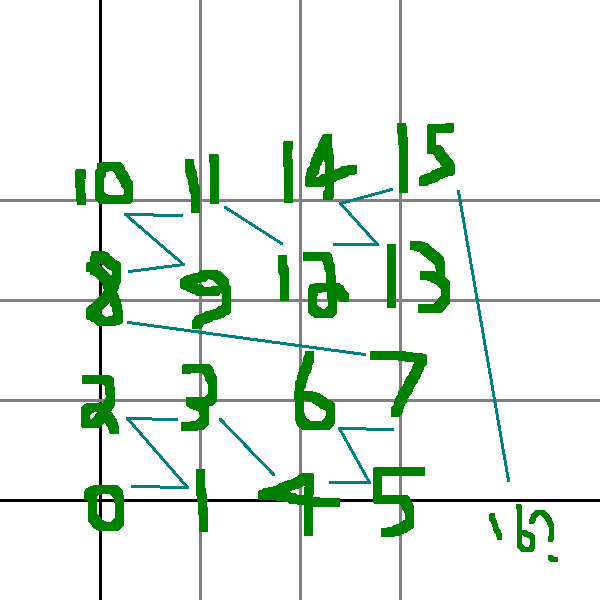
Ooh, there we go. We've found a Z-order curve! (In this case, a backwards Z since the origin is in the bottom left.) I predict that as you plot each x = 0..n, y = 0..n you add another two rows and columns to form a new square of numbers. So (4,0) should map to 16... does it? $$100\ and\ 000 = 010000 = 10000$$ which is indeed 16. It also seems that each column contains even, odd, even integers only, which is reminiscent of our bit interleaving. Perhaps obviously, each Z-square taken as a matrix has determinant of 2.
The graph really helps to convince that this bit-interleaving function is one-to-one without a formal proof. I'm sure a formal proof exists, and I may come back and do one when it's not so late. This technique can also be extended into further dimensions! You can bit-interleave with three integers, four, etc. Dimensionality is an interpretation...
I'm sure there are some deep implications hidden here in terms of efficiently dealing with multi-dimensional (or hyper-dimensional?) entities across multiple machines, and geospatial indexing as an application...
Edit: Here is a function for computing a Morton Number based on the binary representation of the coordinates.
[math](X_2, Y_2) \Rightarrow M = \frac{\displaystyle \sum_{j=1}^{L}(2^{2j}*x_{j-1} + 2^{2j+1}*y_{j-1})}{2^2}[/math]
Where $$X_2$$ and $$Y_2$$ denote that both X and Y are in base 2, $$L$$ is the largest string-length of the binary representations between X and Y, and $$y_i$$ and $$y_i$$ represent bit indices. As an example, consider (4,0).
[math](0b100, 0b0) \Rightarrow M = \frac{2^2*0 + 2^4*0 + 2^6*1 + 2^3*0 + 2^5*0 + 2^7*0}{4} = \frac{64}{4} = 16[/math]
Note that $$L = 3$$ in that example.
This gives us a good starting point for a one-to-one proof. I'll get around to that sometime...
Edit: When I generated the Morton numbers used before, I used a bit twiddling hack in C to do it. (In fact it was a modification of this.) It was bugging me though to be using a limited-size datatype. I wanted to compute the Morton Number of any (x,y) regardless of how big! So here's a Python function to do that:
def tomorton(x,y):
x = bin(x)[2:]
lx = len(x)
y = bin(y)[2:]
ly = len(y)
L = max(lx, ly)
m = 0
for j in xrange(1, L+1):
# note: ith bit of x requires x[lx - i] since our bin numbers are big endian
xi = int(x[lx-j]) if j-1 < lx else 0
yi = int(y[ly-j]) if j-1 < ly else 0
m += 2**(2*j)*xi + 2**(2*j+1)*yi
return m/4
An example:
print morton.tomorton(38923832898389048984895392939448897345932947489293390230538957239479297, 38927593275279479382953735723047307523759237597297)
# Elapsed time for tomorton: 0.00226402282715
# 822436414704783173023379633944766675679282832496695145071589581373733116932512133113544126161851614781345490613573134139932540161620343532035L
Verification that that's the correct M value is left to the reader...
Posted on 2011-09-27 by Jach
Tags: math
Permalink: https://www.thejach.com/view/id/207
Trackback URL: https://www.thejach.com/view/2011/9/playing_with_morton_numbers
Jach
September 19, 2012 12:53:24 PM
I didn't see this back when I wrote this post, but you can prove something is one-to-one if you can prove it is a strictly monotonically increasing function. It's obvious that M satisfies this. Still don't want to do a proof right now though. (Maybe later this month.)
Anonymous
June 17, 2017 03:56:45 PM
Morton number is also one of the function of INTERCAL (which they called "interleave" or "mingle")