A Fun, Dirty, Computer Engineering Comic

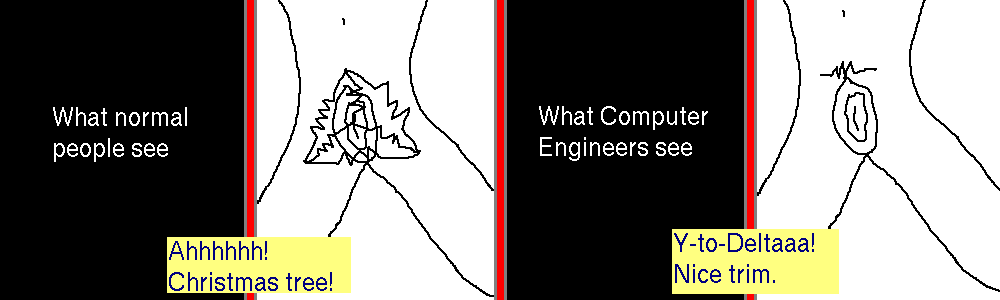
Horrible joke I know, and I suck at drawing, especially "anatomy". Computer Engineers have a trick to convert a bunch of resistors in a delta (triangle) formation to a Y (three prongs) formation and vice versa, and with that trick one can reduce the "hair circuit" shown (that some people apparently call a Christmas tree since it contains both a delta and a Y) to the nice single-resistor trim.

The "Christmas tree" appears in Giancoli, because usually Computer Engineers don't have to deal with it, and Giancoli's "solution" is to write down several equations of Kirchhoff current and voltage laws to reduce the circuit. Yuck! Here is the diagram, they want to know the equivalent resistance between points A and C.



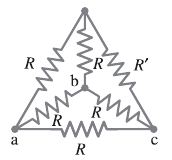
Let's look at the Y-Delta transform equations instead, and see how easy this is. If we transform the inner Y into a Delta, it becomes a problem of resistors in parallel which is trivial. The three equations for the three sides of the Delta:

[math]R_a = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_2}[/math]
[math]R_b = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_3}[/math]
[math]R_c = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1}[/math]

But looking at the actual Y, we see all the resistors are equal to R, making each of the three sides simply equal to 3R. So we end up with a bunch of 3R resistors in parallel with the original sides, and we end up with this reduction.



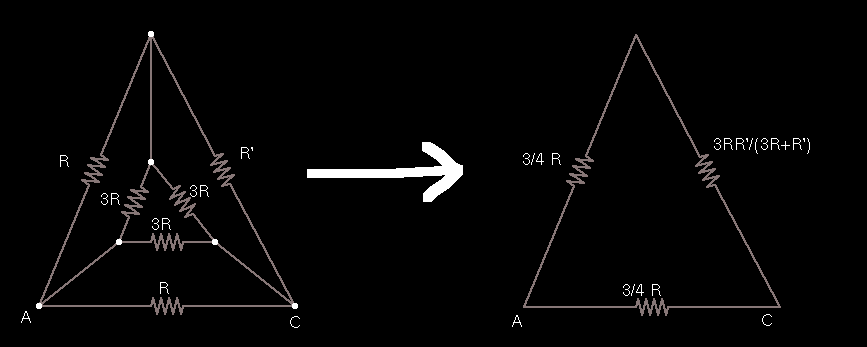
And of course a final single resistor between A and C has the value of R(3R + 5R')/(8(R + R')). Nice trim.

---

Posted on 2011-04-25 by Jach

Tags: circuit analysis, comics, computer engineering

Permalink: https://www.thejach.com/view/id/170

Trackback URL: https://www.thejach.com/view/2011/4/a_fun_dirty_computer_engineering_comic

Back to the top